 The Stochastic Resonance (SR) phenomenon has been discovered and proposed for the first time in 1981 (see
The Stochastic Resonance (SR) phenomenon has been discovered and proposed for the first time in 1981 (see
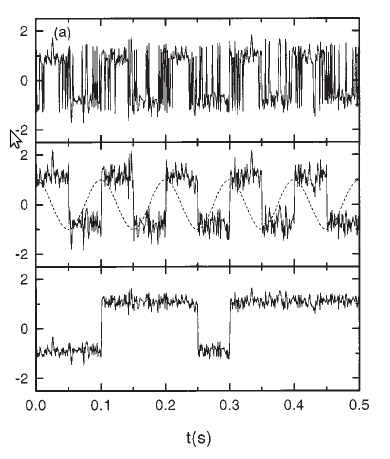
Strictly speaking SR occurs in bistable systems, when a small periodic (sinusoidal) force is applied together with a large wide band stochastic force (noise). The system response is driven by the combination of the two forces that compete/cooperate to make the system switch between the two stable states. The degree of order is related to the amount of periodic motion that it shows in the system response. When the periodic force is chosen small enough in order to not make the system response switch, the presence of a non-negligible noise is required for it to happen. When the noise is small very few switches occur, mainly at random with no significant periodicity in the system response. When the noise is very strong a large number of switches occur for each period of the sinusoid and the system response does not show remarkable periodicity. Quite surprisingly, between these two conditions, there exists an optimal value of the noise that cooperatively concurs with the periodic forcing in order to make almost exactly one switch per period (a maximum in the Signal-to-Noise Ratio).
Such a favorable condition is quantitatively determined by the matching of two time scales: the period of the sinusoid (the deterministic time scale) and the Kramers rate (i.e. the inverse of the average switch rate induced by the sole noise: the stochastic time scale). Thus the name ‘Stochastic Resonance’.
